Пирамида призма менен бирге үч өлчөмдүү мейкиндикте кемчиликсиз көп тараптуу, алардын геометриялык мүнөздөмөлөрү орто мектепте окулат. Бул макалада биз пирамидалар деген эмне, алар кандай элементтерден турат, ошондой эле туура пирамидаларды кыскача мүнөздөйбүз.
Геометриялык фигура пирамида
Геометрия көз карашынан алганда пирамида бир көп бурчтуктан жана бир нече үч бурчтуктан турган мейкиндик фигура. Бул көрсөткүчтү алуу абдан жөнөкөй. Бул үчүн n тарабы бар көп бурчтук алып, андан кийин мейкиндикте көп бурчтуктун тегиздигинде жатпаган ыктыярдуу чекит тандап, көп бурчтуктун ар бир чокусун ушул чекитке туташтырыңыз. Албетте, ушундай жол менен түзүлгөн фигурада бири-бирине бир чокуда туташкан n үч бурчтук болот.
Сүрөттөлгөн фигуранын геометриялык формасын элестетүү үчүн сүрөткө тарталы.

Бул төрт бурчтуу пирамиданы көрсөтүп турат, анын негизитөрт бурчтуу жана каптал бети жалпы чокусу бар төрт үч бурчтуктан түзүлгөн.
Пирамида элементтери
Бардык көп кырдуулар сыяктуу эле пирамида үч түрдүү элементтерден түзүлөт:
- четтери;
- топтор;
- кабырга.
Беттер - фигуранын ички көлөмүн курчап турган мейкиндиктен бөлүп турган тегиздиктердин бөлүктөрү. Пирамиданын негизи n-гондон турган болсо, анда анын беттеринин саны дайыма n+1 болот. Алардын n тарабы үч бурчтуу, ал эми бир тарабы айтылган n-бурчтук негиз болуп саналат.
Чокулар фигуранын үч же андан көп беттери кесилишкен чекиттер. Негизги аймак n чокусун камтыйт, алардын ар бири эки үч бурчтуу бет жана негиз менен түзүлөт. n үч бурчтуктун капталдары бириккен чекит пирамиданын чокусу деп аталат. Ошентип, каралып жаткан фигура n+1 чокуларынан турат.
Четтери - эки бет кесилишкенде пайда болгон түз сызыктар. Ар бир чети анын учунда эки чоку менен чектелген. n-gon негизи бар ар кандай пирамида 2n четинен турат. Бул сандын жарымы, б.а., n, каптал үч бурчтуктардын кесилишинен гана түзүлөт.
Сифралардын мүмкүн болгон түрлөрү
Каралып жаткан фигуранын аталышы негиздеги көп бурчтуктун түрү менен өзгөчө аныкталат. Мисалы, эгерде анын үч бурчу жана үч капталы болсо, анда пирамида үч бурчтуу, төртөө болсо төрт бурчтуу жана башкалар болот.
Көп бурчтук томпок жана ойуу, ошондой эле кадимки жана жалпы түрү болушу мүмкүн. Мунун баары пирамиданын көрүнүшүн да аныктайт.
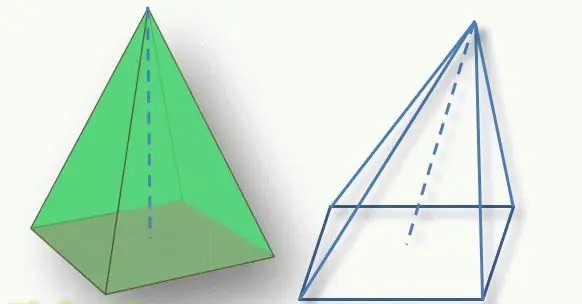
Фигуранын түрүн аныктоодо маанилүү жагдай - бул пирамиданын чокусунун анын негизине салыштырмалуу абалы. Жогору жактан көп бурчтуу негизге тартылган перпендикуляр сегмент фигуранын бийиктиги деп аталат. Эгерде бул сегмент негизди геометриялык борборунда кессе (үч бурчтук үчүн бул медианалардын кесилиши, төрт бурчтук үчүн диагоналдардын кесилиши), анда фигура түз сызык деп аталат. Болбосо, алар жантайыңкы пирамида жөнүндө айтышат.
Эгер пайдубалдын n-гоногу туура (тен жактуу үч бурчтук, квадрат ж.б.) жана фигура түз болсо, анда ал регулярдуу пирамида деп аталат.
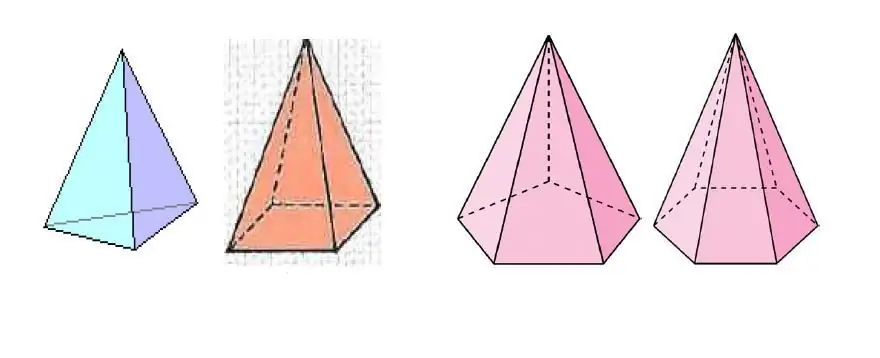
Жогорудагы сүрөттө бир нече пирамидалар көрсөтүлгөн, алар негизи боюнча көп бурчтуктун капталдарынын саны боюнча айырмаланат.
Кадимки пирамидалардын касиеттери
Бул пирамидалар бул класстын башка фигураларынан симметриянын жогорку даражасы менен айырмаланат. Бул жагынан алганда, алар менен ар кандай геометриялык эсептөөлөрдү жүргүзүү ыңгайлуу, мисалы, көлөм же беттин аянты.
Кадимки пирамиданын түбүндө n-гон бар, анын аянты капталынын узундугун билүү менен өзгөчө аныкталат. Фигуранын каптал бети бирдей капталдуу n бирдей үч бурчтуктан түзүлгөн. Каптал бетинде жайгашкан кадимки пирамиданын четтери бири-бирине барабар. Бул четинин узундугунун мааниси көбүнчө фигуранын апотемасын эсептөөдө жана бетинин аянтын аныктоодо колдонулат.
Кадимки пирамиданын бийиктиги - фигуранын экинчи маанилүү мүнөздөмөсү (биринчи - четинин узундугунегиздер). Үндү эсептөөдө бийиктик колдонулат.
Пирамиданын каптал беттерин кескен негизге параллель болгон ар кандай тегиздик көп бурчтуу кесимдин пайда болушуна алып келет. Негизги көп бурчтукка карата гомотетикалык. Сүрөттөлгөн кесүү операциясы жаңы фигуралардын бүтүндөй классын - кесилген кадимки пирамидаларды түзүүгө алып келет.
Эң атактуу пирамидалар

Албетте, булар Египет фараондорунун кадимки төрт бурчтуу пирамидалары. Гиза деген жерде бул таш эстеликтердин 100дөн ашык жасалгасы жана геометриялык параметрлеринин тактыгы бүгүнкү күнгө чейин илимпоздорду таң калтырып келет. Алардын эң чоңу Хеопс пирамидасы, анын бийиктиги 146 метрге, узундугу 230 метрге жакын.
Бул пирамидалар эмне үчүн кызмат кылган, ошондой эле алар кандай механизмдер менен жана качан курулганын бүгүнкү күнгө чейин эч ким билбейт.






