Табигый геометриялык оймо-чиймелер же оймо-чиймелер кайталануучу фигуралар катары көрүнөт, аларды кээде математикалык моделдер менен сүрөттөп же көрсөтүүгө болот.
Табияттагы жана жашоодогу геометрия симметрия, спираль же толкун сыяктуу көптөгөн формаларда жана формаларда болот.
Тарых
Биринчи жолу байыркы грек философтору жана окумуштуулары - Пифагор, Эмпедокл жана Платон жаратылыштагы геометрия маселелерин колго алышкан. Өсүмдүктөрдүн жана жаныбарлардын болжолдуу же идеалдуу геометриялык фигураларынын мисалдарын талдоо менен алар табияттагы тартипти жана симметрияны көрсөтүүгө аракет кылышкан.
Табияттагы геометрияны изилдөөнүн заманбап аракеттери 19-кылымда самын көбүгүнүн минималдуу бети жөнүндөгү концепцияны иштеп чыккан бельгиялык физик Йозеф Платонун аракети менен башталган. Биринчи заманбап аракеттер адегенде идеалдуу жана болжолдуу геометриялык фигураларды көрсөтүүгө топтолгон, андан кийин геометриянын жаратылыштагы көрүнүшүн жана көрүнүшүн алдын ала айткан моделдерди иштеп чыгууга бурулган.
20-кылымда математик Алан Тьюринг жаныбарлардын сырткы көрүнүшүн түшүндүргөн морфогенездин механизмдеринин үстүндө иштеген.ар кандай оймо-чиймелер, тилкелер, тактар. Бир аздан кийин биолог Аристид Линденмайер математик Бенуа Манделброт менен бирге кээ бир өсүмдүктөрдүн, анын ичинде дарактардын өсүү схемаларын кайталаган математикалык фракталдардын үстүндө иштөөнү аяктайт.
Илим
Заманбап илимдер (математика, физика жана химия) технологиялардын жана моделдердин жардамы менен жаратылышта кездешүүчү геометриялык калыптарды түшүндүрүүгө гана эмес, алдын ала айтууга да аракет кылышат.
Павлин, колибри, деңиз кабыктары сыяктуу көптөгөн тирүү организмдердин формасы жана түсү кооз гана эмес, геометриялык жактан да туура болушу окумуштуулардын кызыгуусун жаратат. Табиятта биз байкаган сулуулук табигый, математикалык жол менен пайда болушу мүмкүн.
Математикада байкалган табигый мыйзам ченемдүүлүктөр спиралдар жана фракталдар менен иштеген хаос теориясы менен түшүндүрүлөт. Мындай мыйзам ченемдүүлүктөр физиканын мыйзамдарына баш ийет, андан тышкары физика жана химия абстракттуу математиканы колдонуу менен кристаллдардын табигый да, жасалма дагы формаларын болжолдойт.
Биология табияттагы геометрияны табигый тандалуу аркылуу түшүндүрөт, мында сызыктар, тактар, ачык түстөр сыяктуу үзгүлтүксүз мүнөздөмөлөрдү маскалоо же сигналдарды жөнөтүү зарылчылыгы менен түшүндүрүүгө болот.
Оюналардын түрлөрү
Жаратылышта ар кандай геометриялык фигураларда пайда болгон көптөгөн кайталануучу оймо-чиймелер бар. Жаратылыштагы геометриянын негизги мыйзам ченемдүүлүктөрүнүн түрлөрүн, сүрөттөрүн жана алардын сүрөттөмөлөрүн төмөндө табууга болот.
Симметрия. Бул геометриялык фигура табиятта эң кеңири таралган формалардын бири. Көбүнчө жаныбарларда кездешеткүзгү симметрия - көпөлөктөр, коңуздар, жолборстор, үкүлөр. Ал ошондой эле клен жалбырактары же орхидея гүлдөрү сыяктуу өсүмдүктөрдө кездешет. Мындан тышкары, табияттагы симметриялык геометрия кар бүртүкчөлөрү сыяктуу радиалдык, беш нурлуу же алты эселенген болушу мүмкүн.

Фракталдар. Математикада бул чексиз өзүнө окшош конструкциялар. Жаратылышта мындай чексиз өзүн-өзү кайталануучу форманы табуу мүмкүн эмес, ошондуктан фракталдык схемалардын жакындашуусу жаратылышта геометриялык фракталдар деп аталат. Мындай геометрияны жаратылышта папоротниктин жалбырактарында, брокколиде, ананас мөмөлөрүндө байкоого болот.
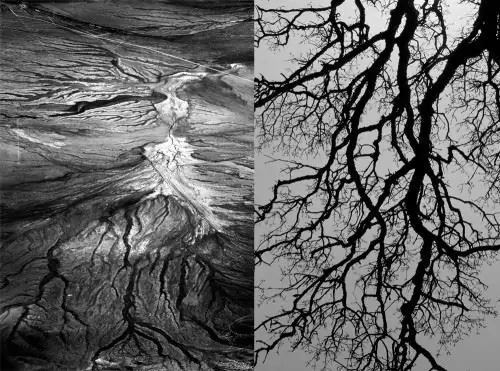
Спиралдар. Бул формалар өзгөчө моллюскалардын жана үлүлдөрдүн арасында кеңири таралган. Окумуштуулар мейкиндикте спиралдык формаларды, мисалы, спиралдык галактикаларды байкашат. Спираль Фибоначчинин алтын катышы деп аталат.

Меандрлар. Математикадагы динамикалык системалардын кокустуктары табиятта меандрлар жана агымдар сыяктуу формаларда көрүнөт. Табигый геометрия дарыянын агымы сыяктуу сынык же тескерисинче ийри сызык түрүндө болот.
Толкундар. Алар аба аркылуу да, суу аркылуу да таралган абанын, шамалдын агымынын бузулушунан жана кыймылынан келип чыгат. Табиятта булар деңиз толкундары гана эмес, геометриялык фигураларды - сызыктарды, жарым ай жана параболаларды түзө алган чөл дөбөлөрү да.
Мозаика. Ошол эле элементтерди бетинде кайталоо менен түзүлгөн. Жапайы жаратылыштагы мозаика геометриясы аарыларда кездешет: алар куратбал уюктары - кайталануучу клеткалар.

Үлгүлөрдү түзүү
Биологияда геометриялык түстүн пайда болушу табигый тандалуу процессине байланыштуу. 20-кылымдын орто ченинде Алан Тьюринг жаныбарлардын түсүндөгү тактардын жана сызыктардын пайда болуу механизмин сүрөттөөгө жетишкен - ал аны реакция-диффузия модели деп атаган. Дененин кээ бир клеткаларында химиялык реакциялар тарабынан башкарылуучу гендер бар. Морфоген кара пигменттүү тери аймактарынын пайда болушуна алып келет (тактар жана сызыктар). Эгерде морфоген бардык тери клеткаларында болсо - пантеранын түсү, ал бирдей эмес болсо - кадимки так илбирс алынат.






