Математикада суммалоо (чоң грек сигма символу менен белгиленет) сандардын суммасынын жыйындысы. суммасы канча? Мына ушундай аракеттин натыйжасы. Эгерде сандар солдон оңго карай биринин артынан бири кошулса, анда ортодогу жыйынтык жарым-жартылай сумма болот.
Суммасы кандай?
Жыйынтыкталуучу сандар бүтүн, рационалдуу, реалдуу же татаал болушу мүмкүн. Аларга кошумча маанилердин башка түрлөрүн кошууга болот: векторлор, матрицалар, көп мүчөлөр жана жалпысынан кандайдыр бир кошумча топтун элементтери (же моноид).
Эгерде терминдердин элементтеринин саны чектүү болсо, анда суммалоо ар дайым так аныкталган маанини берет. Чексиз маанилердин ырааттуулугунун жыйындысы катар деп аталат. Анын маанисин көбүнчө чек аркылуу аныктоого болот (бирок кээде мааниси чексиз болушу мүмкүн).
Секеанстар
Сандардын жыйындысы [3, 7, 2, 1] мааниси ага кирген цифралардын суммасы болгон туюнтма менен аныкталышы мүмкүн, мисалы 3 + 7 + 2 + 1=13. кошумчаассоциативдик түрдө, сумма терминдердин кандайча топтоштурулганына көз каранды эмес, мисалы, (3 + 7) + (2 + 1) жана 3 + ((7 + 2) + 1) экөө тең тогузга барабар, андыктан кашаалар адатта жок кылынат. Кошуу да коммутативдик болуп саналат, ошондуктан шарттарды кайра түзүү сумманын маанисин өзгөртпөйт. Бул касиет чексиз суммада иштебеши мүмкүн экенин эске алыңыз.

Мындай ырааттуулуктарды кошуу үчүн атайын белгилер жок. Эки элементтен аз болсо, бир аз нюанс бар. Бир мүчөнүн ырааттуулугунун жыйындысы плюс белгисин камтыбайт (ал сандын өзүнүн формасынан айырмаланбайт) жана эгерде такыр эле элементтер жок болсо, анда аны жазууга да болбойт (бирок анын ордуна аны төмөнкүчө белгилөөгө болот) анын мааниси "0"). Бирок, ырааттуулуктун шарттары функция сыяктуу белгилүү бир үлгү менен көрсөтүлсө, анда суммалоо оператору пайдалуу же маанилүү болушу мүмкүн.
Жазуу
Сумма эмне экенин түшүнүү үчүн анын сырткы көрүнүшүн талдоо да керек.
1ден 100гө чейинки бүтүн сандардын ырааттуулугун кошуу үчүн көбүнчө жетишпеген мүчөлөрдү көрсөтүү үчүн эллипсти камтыган туюнтма колдонулат: 1 + 2 + 3 + 4 + … + 99 + 100. Үлгү бул мисалда көрүү абдан жеңил. Бирок, татаалыраак варианттар үчүн элементтердин маанисин табуу үчүн колдонулган эрежени так көрсөтүү керек, ага "Σ" кошуу оператору аркылуу жетүүгө болот. Бул белгини (сигма) колдонуп, төмөнкү белгини колдонсоңуз болот:
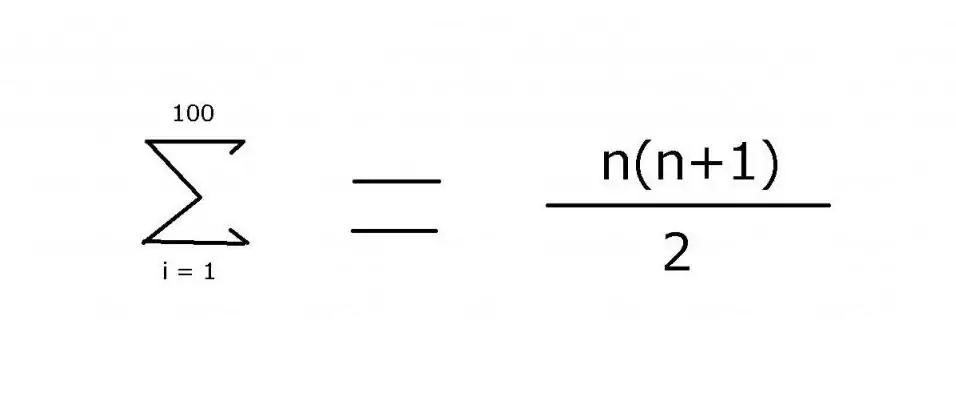
Бул туюнтумдун мааниси 5050. Аны формуланын экинчи бөлүгү келип чыккан математикалык индукциянын жардамы менен тапса болот.
Ар кандай ырааттуулуктар үчүн формула өзгөрөт. Жазуу процесси кандайдыр бир чексиз ырааттуулуктун алдын ала сүрөтүн издөөгө жана аны формула менен сыпаттоого чейин кыскарган. Муну кылгандан кийин, белгилүү бир учурда канча сумма бар экенин түшүнүү кыйын эмес.
Сандардын белгилери менен (плюс же минус) кошуларын тактоо зарыл болгондо алгебралык сумма термини колдонулат. Мисалы, электр чынжырынын теориясында Кирхгофтун чынжыр мыйзамдары түйүнгө кирип-чыгып жаткан токтарга карама-каршы белгилерди берип, бир чекитте жолугушкан өткөргүчтөрдүн тармагындагы токтун алгебралык суммасын карайт.






