Окуучулардын улгайган сайын, жөнөкөй маселелерди чечүүдө тездик талап кылынат. Экзамендерде жөнөкөй мисалдарды же маселелерди чечүү үчүн көп убакыт берилбейт. Квадраттын диагоналын кантип тез жана оңой тапса болот? Бул балдарга сегизинчи класстан баштап үйрөтүлөт. Бул макалада эки жол көрсөтүлөт - бири узунураак, экинчиси тезирээк.
Квадраттын диагоналын кантип эсептөө керек?
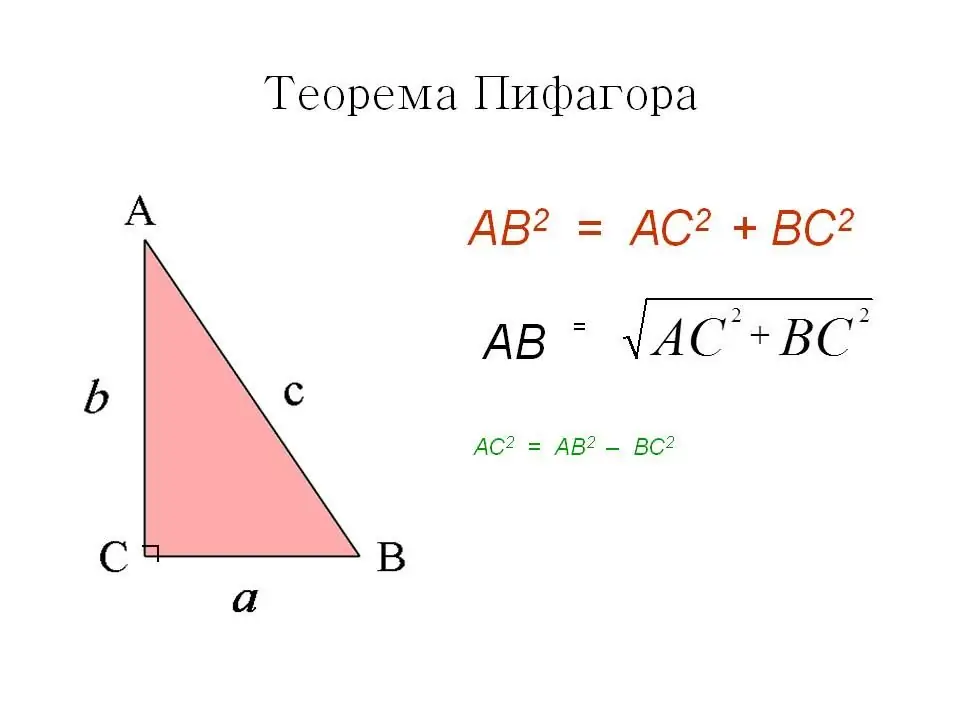
Биринчи жол - бул белгилүү жана тааныш Пифагор теоремасы. Квадраттын бардык бурчтары туура, бул диагонал аны эки бирдей тик бурчтуу үч бурчтукка бөлөт жана өзү алардын гипотенузасы болуп саналат. Пифагор теоремасы боюнча, гипотенузанын квадраты буттардын квадраттарынын суммасына барабар.

Экинчи жол - бул квадраттарга гана таандык жөнөкөй формула жана аны эстеп калуу керек. Белгилүү болгондой, квадраттын бардык тараптары бирдей, ошондуктан математиктер анын диагоналын табуу үчүн төмөнкү формуланы эсептешкен: ал капталынын жана экинин тамырынын көбөйтүндүсүнө барабар.
Албетте, квадраттын диагоналынын узундугунун формуласын эстеп, аны ар дайым колдонгон жакшы, анткени ал бир топ ылдам жана ыңгайлуу. Бул, өзгөчө, көйгөйлөрдү түз түрдө чечкенде сезилет, мында бүтүндөй чоң тамыр туюнтмаларынын ордуна бир гана продукт менен иштей аласыз.
Мисалы
Мисалы, 6х6 квадратты алалы, башкача айтканда, капталы алты сантиметрге барабар.
Биринчи ыкма боюнча: диагоналы C, капталы A болсун.
Анда биз C=√A^2+A^2 же C=√2A^2 деп алабыз.
Сан түрүндө жазалы: С=√36 + 36. Биз √72 алдык, ал 3√8 же 6√2.
Эми ошол эле диагоналды табалы, бирок экинчи ыкма менен: C=A√2 же сан түрүндө: 6√2
Эми экинчи ыкма канчалык тезирээк, оңой жана эң негизгиси - эффективдүүрөөк экенин, өзгөчө ушундай жеңил маселелерди чечүүдө көрө аласыз, анткени сынакта ар бир мүнөт кымбат!
Квадрат диагоналдардын башка касиеттери
Квадраттын диагоналдарын табуудан тышкары, алардын касиеттерин да билишиңиз керек. Негизгилери:
- Диагоналдары бири-бирине барабар жана кесилишкен чекити экиге бөлүнгөн.
- Алар кесилишкенде тик бурчтарды түзөт.
- Квадратты бирдей үч бурчтуктарга бөлүңүз.
Тыянак
Квадраттын диагоналдарын кантип санайбыз деген суроону көбүнчө мектепте бул теманы өткөрүп жиберген окуучулар беришет. Бирок, ар бир адам математиканын мындай фундаменталдуу эрежелерин билиши керек! Мүмкүн болушунча тезирээк чечүү максатка ылайык, бул үчүн кыскартылган формулаларды билүү талап кылынат. Мунун баары өтө жөнөкөй жана жеңил, бирокошону менен бирге ал келечекте алда канча татаал проблемаларды чечуу учун зарыл негиз болуп саналат. Жана бул базанын маанилүү бөлүгү квадрат болуп саналат.






