Белгилүү болгондой, ар кандай физикалык чоңдук эки түрдүн бирине таандык, ал скаляр же вектор. Бул макалада биз ылдамдык жана ылдамдануу сыяктуу кинематикалык мүнөздөмөлөрдү карап чыгабыз, ошондой эле ылдамдануу жана ылдамдык векторлору кайда багытталганын көрсөтөбүз.
Ылдамдык жана ылдамдануу деген эмне?
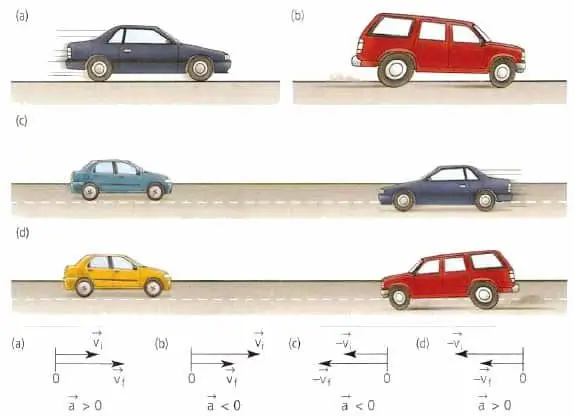
Бул абзацта айтылган эки чоңдук тең кыймылдын бардык түрүнүн маанилүү мүнөздөмөлөрү болуп саналат, мейли ал денени түз сызыкта же ийри жол менен жылдырса.
Ылдамдык - убакыттын өтүшү менен координаттардын өзгөрүү ылдамдыгы. Математикалык жактан бул маани басып өткөн жолдун убакыттын туундусуна барабар, башкача айтканда:
v¯=dl¯/dt.
Бул жерде l¯ вектору жолдун башталышынан акыркы чекитине чейин багытталган.
Өз кезегинде, ылдамдануу - ылдамдыктын өзү убакыттын өтүшү менен өзгөргөн ылдамдыгы. Формула түрүндө аны төмөнкүчө жазса болот:
a¯=dv¯/dt.
Албетте, экинчи туунду алыпжылышуу вектору l¯ убакыттын өтүшү менен, биз ылдамдануунун маанисин да алабыз.
Ылдамдык секундасына метр менен ченелгендиктен, ылдамдануу, жазылган сөзгө ылайык, секундасына метр квадрат менен ченелет.

Ылдамдануу жана ылдамдык векторлору кайда?
Физикада дененин ар кандай механикалык кыймылы адатта белгилүү бир траектория менен мүнөздөлөт. Акыркысы дене мейкиндикте кыймылдаган кандайдыр бир элестүү ийри сызык. Мисалы, түз сызык же тегерек - жалпы кыймыл жолдорунун эң сонун мисалдары.
Дененин ылдамдыгынын вектору дененин жайлап же ылдамдагандыгына, түз сызыкта же ийри сызык боюнча кыймылдаганына карабастан, дайыма кыймыл багытына багытталган. Геометриялык терминдер менен айтсак, ылдамдык вектору дене учурда жайгашкан траекториянын чекитине тангенциалдуу багытталат.
Материалдык же дене чекитинин ылдамдануу векторунун ылдамдыкка эч кандай тиешеси жок. Бул вектор ылдамдыктын өзгөрүү багытында багытталган. Мисалы, түз сызыктуу кыймыл үчүн a¯ мааниси же v¯ менен багытта дал келиши же v¯ге карама-каршы болушу мүмкүн.
Денеге таасир этүүчү күч жана ылдамдануу
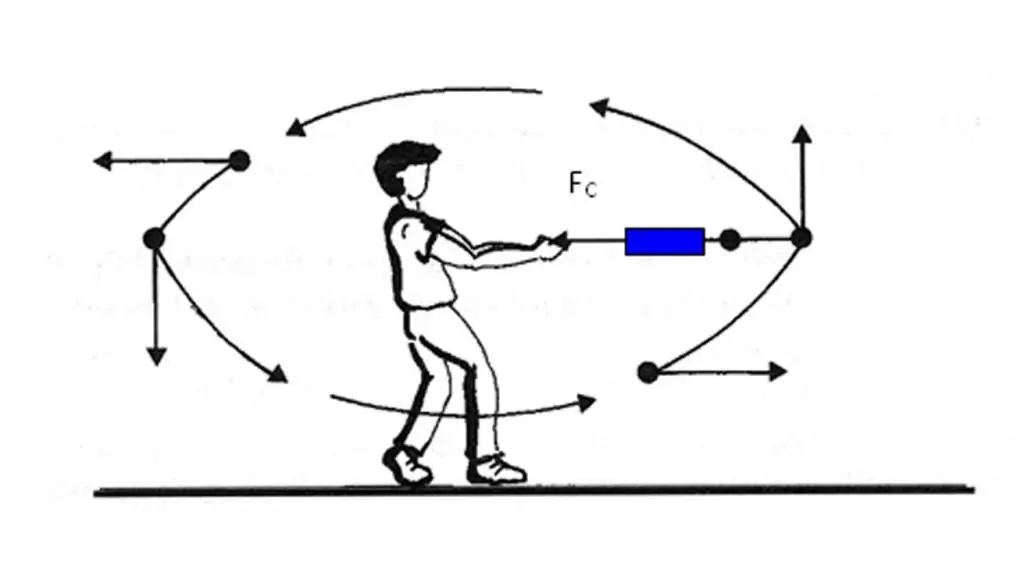
Биз дененин ылдамдануу вектору ылдамдык векторунун өзгөрүшүнө багытталганын аныктадык. Бирок траекториянын берилген чекитинде ылдамдык кандай өзгөрөрүн аныктоо дайыма эле оңой боло бербейт. Анын үстүнө ылдамдыктын өзгөрүшүн аныктоо үчүн операцияны аткаруу кереквектордук айырмачылыктар. a¯ векторунун багытын аныктоодо мындай кыйынчылыктарды болтурбоо үчүн, тезирээк аныктоонун дагы бир жолу бар.
Төмөндө Ньютондун белгилүү жана ар бир окуучуга белгилүү мыйзамы:
F¯=ma¯.
Формула денелердеги ылдамдануунун себеби аларга таасир этүүчү күч экенин көрсөтүп турат. m массасы скаляр болгондуктан, күч вектору F¯ менен ылдамдануу вектору a¯ бир багытта. Бул фактыны эстен чыгарбоо жана иш жүзүндө колдонуу зарыл болгон учурда, а¯ чоңдуктун багытын аныктоо зарыл.
Эгер денеге бир нече түрдүү күчтөр таасир этсе, анда ылдамдануу векторунун багыты бардык күчтөрдүн пайда болгон векторуна барабар болот.
Айланма кыймыл жана ылдамдануу
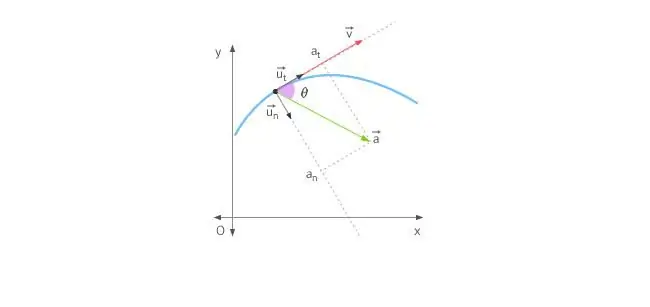
Дене түз сызыкта кыймылдаганда, ылдамдануу алдыга же артка багытталат. Тегерек боюнча кыймыл болгон учурда ылдамдык вектору өз багытын тынымсыз өзгөртүп тургандыктан абал татаалдашат. Жогоруда айтылгандарды эске алуу менен, жалпы ылдамдануу анын эки компоненти менен аныкталат: тангенциалдык жана нормалдуу ылдамдануулар.
Тангенциалдык ылдамдануу так ылдамдык вектору менен бирдей же ага каршы багытталган. Башкача айтканда, бул ылдамдануу компоненти траекторияга тангенс боюнча багытталган. Тангенциалдык ылдамдануу ылдамдыктын модулунун өзгөрүшүн сүрөттөйт.
Нормалдуу ылдамдануу анын ийрилигин эске алуу менен траекториянын берилген чекитине нормал боюнча багытталат. Айланма кыймылда бул компоненттин вектору көрсөтөтборборго, башкача айтканда, нормалдуу ылдамдануу айлануу радиусу боюнча багытталган. Бул компонент көбүнчө центрипеталдык деп аталат.
Толук ылдамдануу бул компоненттердин суммасы, андыктан анын вектору тегерек сызыгына карата ыктыярдуу багытталышы мүмкүн.
Эгер дене сызыктуу ылдамдыкты өзгөртпөстөн айланса, анда нөлдөн башка нормалдуу компонент гана бар, ошондуктан толук ылдамдануу вектору айлананын борборуна багытталган. Бул борборго денени өз траекториясында кармап турган күч да таасир этээрин эске алыңыз. Мисалы, Күндүн тартылуу күчү биздин Жерди жана башка планеталарды өз орбиталарында кармап турат.






